Question

Let f(x) = x^2 + 6x.

(A) Find the slope of the secant line joining (3,f(3)) and (9,f(9)).
(B) Find the slope of the secant line joining (5,f(5)) and (5+h,f(5+h)).

Answer 1

(A) The slope of secant line is 18.

(B) The slope of secant line is h+16.

Explanation:

(A)

The given function is

`f(x)=x^2+6x`

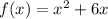
At x=3,

`f(3)=(3)^2+6(3)=27`

At x=9,

`f(9)=(9)^2+6(9)=135`

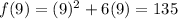
The secant line joining (3,27) and (9,135). So, the slope of secant line is

`m=(y_2-y_1)/(x_2-x_1)`

`m=(135-27)/(9-3)=18`

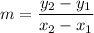
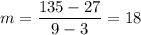
The slope of secant line is 18.

(B)

The given function is

`f(x)=x^2+6x`

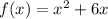
At x=5,

`f(5)=(5)^2+6(5)=55`

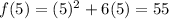
At x=5+h,

`f(5+h)=(5+h)^2+6(5+h)=h^2 + 16 h + 55`

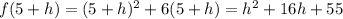
The secant line joining (5,55) and
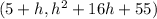`(5+h,h^2 + 16 h + 55)`. So, the slope of secant line is

`m=(h^2 + 16 h + 55-55)/(5+h-5)`

`m=(h^2 + 16 h )/(h)`

`m=h+16`

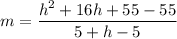
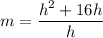
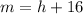
The slope of secant line is h+16.