Answer:
(A) The slope of secant line is 18.
(B) The slope of secant line is h+16.
Explanation:
(A)
The given function is
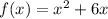
At x=3,
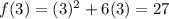
At x=9,
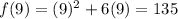
The secant line joining (3,27) and (9,135). So, the slope of secant line is
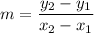
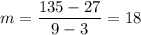
The slope of secant line is 18.
(B)
The given function is
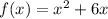
At x=5,
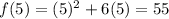
At x=5+h,
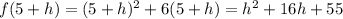
The secant line joining (5,55) and
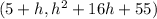 . So, the slope of secant line is
. So, the slope of secant line is
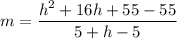
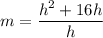
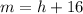
The slope of secant line is h+16.