Answer:
False. See te explanation an counter example below.
Explanation:
For this case we need to find:
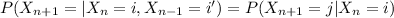 for all
for all
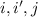 and for
and for
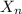 in the Markov Chain assumed. If we proof this then we have a Markov Chain
in the Markov Chain assumed. If we proof this then we have a Markov Chain
For example if we assume that
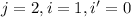 then we have this:
then we have this:
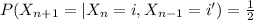
Because we can only have
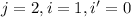 if we have this:
if we have this:
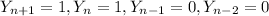 , from definition given
, from definition given
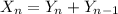
With
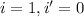 we have that
we have that
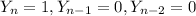
So based on these conditions
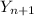 would be 1 with probability 1/2 from the definition.
would be 1 with probability 1/2 from the definition.
If we find a counter example when the probability is not satisfied we can proof that we don't have a Markov Chain.
Let's assume that
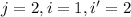 for this case in order to satisfy the definition then
for this case in order to satisfy the definition then
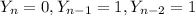
But on this case that means
 and on this case the probability
and on this case the probability
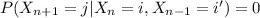 , so we have a counter example and we have that:
, so we have a counter example and we have that:
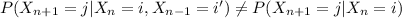 for all
for all
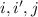 so then we can conclude that we don't have a Markov chain for this case.
so then we can conclude that we don't have a Markov chain for this case.