Answer:
The range of g(x) will be all real numbers less than zero.
Explanation:
The graph of
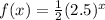 and its reflection across the x-axis, g(x), are given.
and its reflection across the x-axis, g(x), are given.
Now, another function g(x) will be given by
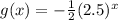 ............ (1)
............ (1)
Since by reflection across the x-axis the curve will change its y-value only by sign and the x-value remains the same.
Now, g(x) approaches y = 0 in quadrant 3 and decreases into quadrant 4. It crosses the y-axis at (0,-0.5) and goes through (2,-3).
Therefore, the range of the equation (1) will be all real numbers less than zero. (Answer)