Answer:
1:8
Explanation:
Given that in square ABCD, point M is the midpoint of side AB and point N is the midpoint of side BC.
Let the side of the square be a.
Area of square ABCD =
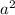
The triangle AMN is having two legs of a right triangle as half of side of the square
i.e. Triangle AMN has base = height = a/2
So area of triangle AMN =
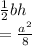
Ratio of the area of triangle AMN to area of square ABCD
= 1:8