Answer:
3
Explanation:
Mean refers to the average value of the set of data.
It is the central value of the set of data.
Another word for Mean is average.
Given scores:7, 9, 6, 3, 7, 8, 4, 10, 7, 9
Solution:
Sum of observations =
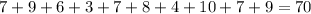
Number of observations = 10
Mean = Sum of observations/Number of observations =

If observation 3 is removed:
Sum of observations =
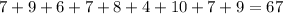
Number of observations = 9
Mean = Sum of observations/Number of observations =

If observation 4 is removed:
Sum of observations =
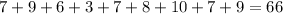
Number of observations = 9
Mean =
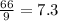
If observation 6 is removed:
Sum of observations =
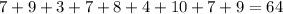
Number of observations = 9
Mean =
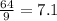
If observation 7 is removed:
Sum of observations =
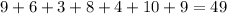
Number of observations = 7
Mean =
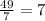
If observation 8 is removed:
Sum of observations =
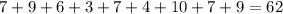
Number of observations = 9
Mean =
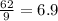
If observation 9 is removed:
Sum of observations =
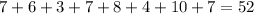
Number of observations = 8
Mean =
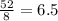
If observation 10 is removed:
Sum of observations =
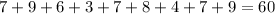
Number of observations = 9
Mean =
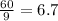
Therefore, mean of this distribution of scores would be changed the most if a score 3 was removed from the data set.