Question

Imagine that you have entered the following distribution of scores into the program: 7, 9, 6, 3, 7, 8, 4, 10, 7, 9. The mean of this distribution of scores would be changed the most if a score of ________ was removed from the data set.

Answer 1

3

Explanation:

Mean refers to the average value of the set of data.

It is the central value of the set of data.

Another word for Mean is average.

Given scores:7, 9, 6, 3, 7, 8, 4, 10, 7, 9

Solution:

Sum of observations =
`7+ 9+ 6+ 3+ 7+ 8+ 4+ 10+ 7+ 9=70`

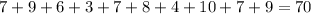
Number of observations = 10

Mean = Sum of observations/Number of observations =
`(70)/(10)=7`

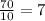
If observation 3 is removed:

Sum of observations =
`7+ 9+ 6+ 7+ 8+ 4+ 10+ 7+ 9=67`

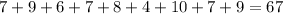
Number of observations = 9

Mean = Sum of observations/Number of observations =
`(67)/(9)=7.44`

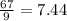
If observation 4 is removed:

Sum of observations =
`7+ 9+ 6+ 3+ 7+ 8+ 10+ 7+ 9=66`

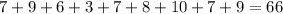
Number of observations = 9

Mean =
`(66)/(9)=7.3`

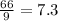
If observation 6 is removed:

Sum of observations =
`7+ 9+ 3+ 7+ 8+ 4+ 10+ 7+ 9=64`

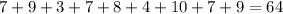
Number of observations = 9

Mean =
`(64)/(9)=7.1`

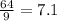
If observation 7 is removed:

Sum of observations =
`9+ 6+ 3+ 8+ 4+ 10+ 9=49`

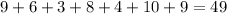
Number of observations = 7

Mean =
`(49)/(7)=7`

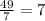
If observation 8 is removed:

Sum of observations =
`7+ 9+ 6+ 3+ 7+ 4+ 10+ 7+ 9=62`

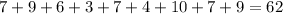
Number of observations = 9

Mean =
`(62)/(9)=6.9`

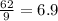
If observation 9 is removed:

Sum of observations =
`7+ 6+ 3+ 7+ 8+ 4+ 10+ 7=52`

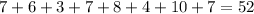
Number of observations = 8

Mean =
`(52)/(8)=6.5`

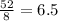
If observation 10 is removed:

Sum of observations =
`7+ 9+ 6+ 3+ 7+ 8+ 4+ 7+ 9=60`

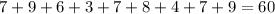
Number of observations = 9

Mean =
`(60)/(9)=6.7`

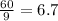
Therefore, mean of this distribution of scores would be changed the most if a score 3 was removed from the data set.