Question

On a vacation flight, you look out the window of the jet and wonder about the forces exerted on the window. Suppose the air outside the window moves with a speed of approximately 200 m/s shortly after takeoff, and that the air inside the plane is at atmospheric pressure. Find the pressure difference between the inside and outside of the window and if the window is 26 cm by 45 cm, find the force exerted on the window by air pressure.

Answer 1

The pressure difference is 25.8kPa while the force exerted on the window by air pressure is 3.02 kN

Step-by-step explanation:

Using the Bernoulli's equation

`P_(in)+(1)/(2)\rho v_(in)^2=P_(out)+(1)/(2)\rho v_(out)^2`

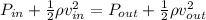
Here

• Pin-Pout is the pressure difference which is to be calculated.

• ρ is the density of air whose value is 1.29 kg/m^3

• vin is the velocity of air inside which is 0 m/s

• vout is the velocity of air outside which is 200 m/s

Substituting values in the above equation yields

`\Delta P=P_(in)-P_(out)\\\Delta P=(1)/(2)\rho (v_(in)^2-v_(out)^2)\\\Delta P=(1)/(2)* 1.29 ( 200^2-0)\\\Delta P=25.8 kPa`

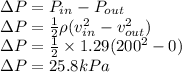
So the pressure difference is 25.8kPa.

As force is given by

`F=PA\\F=\Delta P A\\`

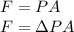
Here

• ΔP is the pressure difference calculated above
• A is the area of the window given as

`A=L * W\\A=0.26 * 0.45\\A=0.117 m^2`

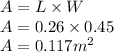
Now force is

`F=\Delta P A\\F=25.8 \tiems 10^3 * 0.117\\F=3.02 kN`

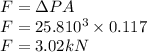
So the force exerted on the window by air pressure is 3.02 kN