Question

How many ways are there to paint a set of 27 27 elements such that 7 7 are painted white, 6 6 are painted old gold, 2 2 are painted blue, 7 7 are painted yellow, 5 5 are painted green, and 0 0 of are painted red?

Answer 1

There are 2,480,721,300,000,00 ways to paint this set.

Explanation:

We have that:

A set of 27 elements, of which:

7 are painted white

6 are painted old gold

2 are painted blue

7 are painted yellow

5 are painted green

How many ways are there to paint?

A single change in the set, for example, element 0 exchanged with element 1, means we have a new way. So we use the permutations formula to solve this problem:

Permutations

Permutations of a set of x elements divided into sets of size w,y,z.

The number of ways is:

`P{x}_(w,y,z) = (x!)/(w!y!z!)`

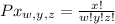
In this problem, we have that:

A set of 27 divided into sets of 7,6,2,7,5. So

`P{27}_(7,6,2,7,5) = (27!)/(7!6!2!7!5!) = 2,480,721,300,000,00`

There are 2,480,721,300,000,00 ways to paint this set.