Answer:
22.6 ft
Explanation:
We are given that
Width of parabola=32 ft
Half width of parabola=
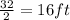
Distance from origin on right side on x-axis=16ft
Distance from origin on left side =-16 ft
Maximum height of parabola=16 ft
Therefore, the point (0,16) lie on the parabola.
Equation of parabola along y-axis is given by

Where vertex=(h,k)
Vertex of parabola=(0,16)
Substitute the value of vertex
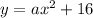 ..(1)
..(1)
Equation(1) is passing through the point (16,0)
Therefore,
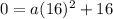
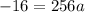
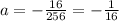
Substitute the value of a in equation(1)
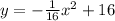
Height of doorway=8 ft
It means we have to find the value of x at y=8
Substitute the value of y
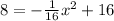
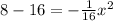
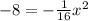
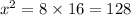
 ft
ft
Width of rectangular doorway=2x=2(11.3)=22.6 ft
Hence, the width of rectangular doorway=22.6 ft