Question

The front of an aircraft hanger is being built in the shape of a parabola, which is 32 ft. wide, and has a maximum height of 16 ft., AND must have a rectangular doorway that is 8 ft. tall. What is the maximum width of the doorway?

Answer 1

22.6 ft

Explanation:

We are given that

Width of parabola=32 ft

Half width of parabola=
`(32)/(2)=16ft`

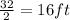
Distance from origin on right side on x-axis=16ft

Distance from origin on left side =-16 ft

Maximum height of parabola=16 ft

Therefore, the point (0,16) lie on the parabola.

Equation of parabola along y-axis is given by

`y=a(x-h)^2+k`

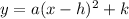
Where vertex=(h,k)

Vertex of parabola=(0,16)

Substitute the value of vertex

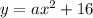`y=ax^2+16`..(1)

Equation(1) is passing through the point (16,0)

Therefore,
`0=a(16)^2+16`

`-16=256a`

`a=-(16)/(256)=-(1)/(16)`

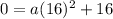
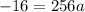
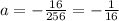
Substitute the value of a in equation(1)

`y=-(1)/(16)x^2+16`

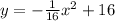
Height of doorway=8 ft

It means we have to find the value of x at y=8

Substitute the value of y

`8=-(1)/(16)x^2+16`

`8-16=-(1)/(16)x^2`

`-8=-(1)/(16)x^2`

`x^2=8* 16=128`

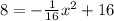
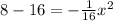
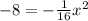
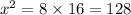
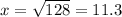`x=√(128)=11.3`ft

Width of rectangular doorway=2x=2(11.3)=22.6 ft

Hence, the width of rectangular doorway=22.6 ft