Answer: The proportion of new car buyers that trade in their old car has statistically significantly decreased.
Explanation:
Since we have given that
p = 48% = 0.48
n = 115
x = 46
So,
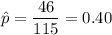
So, hypothesis would be
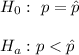
So, test value would be
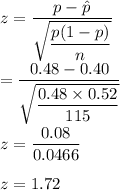
At 10% level of significance, critical value would be
z= 1.28
Since 1.28 < 1.72
So, we will reject the null hypothesis.
Hence, the proportion of new car buyers that trade in their old car has statistically significantly decreased.