Question

Help please! 10 pts
if mBAD =22, what is x?

Answer 1

Answer: x = 136 degrees

Explanation:

The given quadrilateral ABCD is a rectangle. In a triangle, the opposite sides are equal. Also, the diagonals are equal and bisect each other at the midpoint. Let the midpoint be E. It means that AE and BE are equal and ∆ AEB is an isosceles triangle.

Therefore,

m∠DAB and m∠CBA are equal

The sum of the angles in a triangle is 180 degrees. Therefore

m∠ABC + m∠BAD + m∠AEB = 180

22 + 22 + m∠AEB = 180

m∠AEB = 180 - 22 - 22 = 136 degrees

m∠AEB and x are vertically opposite and vertically opposite angle are equal. Therefore

x = 136 degrees

Answer 2

The value of
`x^(0) = 136^(0)`.

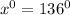Explanation:

The figure provided to is a rectangle, named ABDC.

All the angles of the rectangle, m∠CAB, m∠ABD, m∠BDC and m∠DCA are
`90^(0)`.

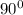The lines AD and BC are diagonals of the rectangle ABDC.

Let the point where the two diagonals intersect be E.

According to the diagonal property of rectangles, they bisect each other.

Then,

• m∠CED = m∠AEB and m∠BED = m∠AEC
• AE = BE, CE = ED
• The opposite angle at the points where the diagonals meet are congruent, i.e. m∠DAB = m∠ADC and m∠DCB = m∠ABC.

Now, consider the triangle ABE.

Since the triangle ABE has two equal sides, i.e. AE = BE, it is an isosceles triangle. And hence the angles m∠EAB= m∠ABE.

Compute the value of m∠BEA using the sum of angles property of a triangle i.e. the sum of all three angles of a triangle is
`180^(0)`.

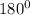m∠EAB+ m∠ABE+ m∠BEA =
`180^(0)`

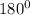
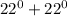`22^(0)+22^(0)` + m∠BEA =
`180^(0)`

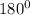
m∠BEA =
`180^(0)-44^(0)\\`

=
`136^(0)`

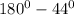
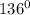
Now, since the diagonals bisect each other m∠CED = m∠AEB.

So,
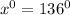`x^(0) = 136^(0)`.