102 gallons of 55 % pure antifreeze and 68 gallons of 80 % pure antifreeze is mixed to obtain 170 gallons of a mixture that contains 65% pure anti-freeze
Solution:
Let "x" be the gallons of 55 % pure antifreeze
Then, (170 - x) be the gallons of 80 % pure antifreeze
Then we can say, according to question,
"x" gallons of 55 % pure antifreeze is mixed with (170 - x) gallons of 80 % pure antifreeze to obtain 170 gallons of a mixture that contains 65% pure anti-freeze
Thus, we frame a equation as:
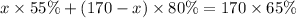
Solve the above expression for "x"

Thus, 102 gallons of 55 % pure antifreeze is used
Then, 170 - x = 170 - 102 = 68 gallons of 80 % pure antifreeze is used
Thus, 102 gallons of 55 % pure antifreeze and 68 gallons of 80 % pure antifreeze is mixed to obtain 170 gallons of a mixture that contains 65% pure anti-freeze