Answer:
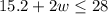
Explanation:
Let w represent width of the rope-off section.
We have been given that a manager needs to rope off a rectangular section for a private party the length of the section must be 7.6 m the manager can use no more than 28 m of the rope.
We will use perimeter of rectangle formula to solve our given problem. We know that perimeter of a rectangle is equal to 2 times the sum of length and width.

Upon substituting our given values, we will get:

Since the manager can use no more than 28 m of the rope, so perimeter of rope-off section should be less than or equal to 28 meters.
We can represent this information in an inequality as:
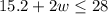
Therefore, our required inequality would be
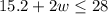 .
.
Let us find width as:
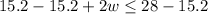

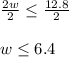
Therefore, the width of the rope-off section should be less than or equal to 6.4 meters.