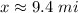Question

Hurry plz. If you can plz show work. Drawing a picture might help

Answer 1

Answer:
`9.4\ miles`

Explanation:

You can draw a Right triangle, as the one shown in the picture attached, where "x" is the distance between Troy and his starting point.

You need to use the Pythagorean Theorem. This is:

`a^2=b^2+c^2`

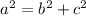
Where "a" is the hypotenuse, and "b" and "c" are the legs of the Right triangle.

In this case, you can identify that the legs of the Right triangle are:

`a=x\\\\b=8\ mi\\\\c=5\ mi`

Therefore, you can substitute values into
`a^2=b^2+c^2` :

`x^2=(8\ mi)^2+(5\ mi)^2`

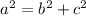Now you need to solve for "x" in order to find its value. This is:

`x=√((8\ mi)^2+(5\ mi)^2)\\\\x=9.43\ mi`

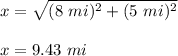
Finally, rounding the result to the nearest tenth of a mile, you get:

`x\approx9.4\ mi`