Answer:
The value of
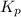 is 0.02495.
is 0.02495.
Step-by-step explanation:
Initial concentration of
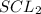 gas = 0.675 M
gas = 0.675 M
Initial concentration of
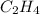 gas = 0.973 M
gas = 0.973 M
Equilibrium concentration of mustard gas = 0.35 M
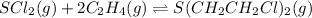
initially
0.675 M 0.973 M 0
At equilibrium ;
(0.675-0.35) M (0.973-2 × 0.35) M 0.35 M
The equilibrium constant is given as :
![K_c=([S(CH_2CH_2Cl)_2])/([SCl_2][C_2H_4]^2)](https://img.qammunity.org/2021/formulas/chemistry/college/c7tjcnuw1dwbwil1rset02zrest7x8vyr3.png)
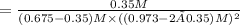
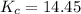
The relation between
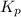 and
and
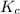 are :
are :
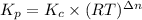
where,
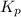 = equilibrium constant at constant pressure = ?
= equilibrium constant at constant pressure = ?
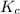 = equilibrium concentration constant =14.45
= equilibrium concentration constant =14.45
R = gas constant = 0.0821 L⋅atm/(K⋅mol)
T = temperature = 20.0°C =20.0 +273.15 K=293.15 K
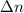 = change in the number of moles of gas = [(1) - (1 + 2)]=-2
= change in the number of moles of gas = [(1) - (1 + 2)]=-2
Now put all the given values in the above relation, we get:
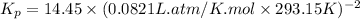
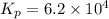
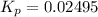
The value of
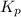 is 0.02495.
is 0.02495.