Question

A tree double in weight in three months. How long will it take to be 1600% in weight? (Linear or exponential growth?)

Answer 1

Answer: 12 months

Explanation:

Given : A tree double in weight in three months.

Since the weight is increasing by growth factor of 2 , therefore its is an exponential growth.

The exponential growth equation is given by :-

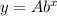`y=Ab^x` (1)

, where A is the initial values , b is the growth factor and x is the time period.

As per given , b= 2

Since the tree doubles in weight in three months, so time period x =
`(t)/(3)` , where t= number of months.

Substitute the value of b and x in (1) , we get

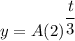`y=A(2)^{(t)/(3)}` , where y= weight of tree after t months and A is initial weight of tree.

When it will be 1600% of his initial weight , the weight of tree : y= 1600% of A =
`(1600)/(100)* A=16A`

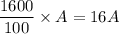
At y= 16 A ,
`16A=A(2)^{(t)/(3)}`

`\Rightarrow\ 16=2^{(t)/(3)}`

`\Rightarrow\ 2^(4)=2^{(t)/(3)}`

`\Rightarrow\ 4=(t)/(3)\Rightarrow\ t=3*4=12`

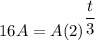
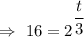
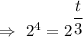
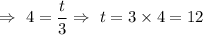
Hence, it will take 12 months to be 1600% in weight.