![\cos (5 \pi) \sin (8 \pi)=(1)/(2)[\sin 13 \pi+\sin (3 \pi)]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/ru1rw9ia1yzgnp5hul2agogl4t2myxrfb1.png) is the answer.
is the answer.
Step-by-step explanation:
To write the product
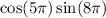 as the sum using product-sum identities.
as the sum using product-sum identities.
The product-sum identity for
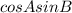 is given by
is given by
![\cos A \sin B=(1)/(2)[\sin (A+B)-\sin (A-B)]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/19pqlsbuboz7dhnfkfz6lv0xg2y8umj4g6.png)
Now, we shall substitute the value for A and B in this formula.
Thus,
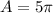 and
and
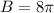 , we have,
, we have,
![\cos (5 \pi) \sin (8 \pi)=(1)/(2)[\sin (5 \pi+8 \pi)+\sin (5 \pi-8 \pi)]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/vthpuk6n0qp24o74yvkxx58wf4ov7t29tv.png)
Adding the terms within the bracket,
![\cos (5 \pi) \sin (8 \pi)=(1)/(2)[\sin 13 \pi-\sin (-3 \pi)]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/w6wycbj4ke33orpfqdweliwks0qmxqogu4.png)
Since, we know that
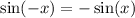 , we have,
, we have,
![\cos (5 \pi) \sin (8 \pi)=(1)/(2)[\sin 13 \pi+\sin (3 \pi)]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/ru1rw9ia1yzgnp5hul2agogl4t2myxrfb1.png)
Thus, the solution is
![\cos (5 \pi) \sin (8 \pi)=(1)/(2)[\sin 13 \pi+\sin (3 \pi)]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/ru1rw9ia1yzgnp5hul2agogl4t2myxrfb1.png)