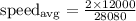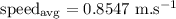Answer:
a)
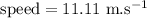
b)
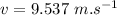
c)
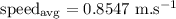
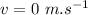
Step-by-step explanation:
Given:
- distance from home to university as measured by the odometer,
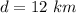
- times taken to cover this distance,
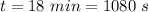
a)
average speed:
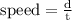
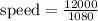
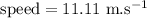
b)
given that displacement,
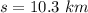
Therefore velocity:
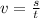

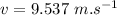
c)
time taken in returning,

Therefore total time in the round trip,
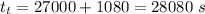
After returning home the total displacement is zero so, average velocity:
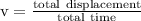
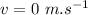
And the average speed: