Question

You are standing in a building whose height (40m) you throw a ball downward at a angle of -30 at a speed of (10m/s) acceleration of gravity is -9.81 m/sec^2

Answer 1

Answer: 3.41 s

Step-by-step explanation:

Assuming the question is to find the time
`t` the ball is in air, we can use the following equation:

`y=y_(o)+V_(o)sin \theta t-(1)/(2)gt^(2)`

Where:

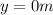`y=0m` is the final height of the ball

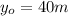`y_(o)=40 m` is the initial height of the ball

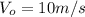`V_(o)=10 m/s` is the initial velocity of the ball

`t` is the time the ball is in air

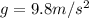`g=9.8 m/s^(2)` is the acceleration due to gravity

`\theta=30\°`

Then:

`0 m=40 m+(10 m/s)(sin(30\°))t-(1)/(2)9.8 m/s^(2)t^(2)`

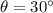
`0 m=40 m+5m/s t-4.9 m/s^(2)t^(2)`

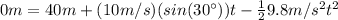
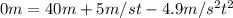
Multiplying both sides of the equation by -1 and rearranging:

`4.9 m/s^(2)t^(2)-5m/s t-40 m=0`

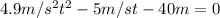
At this point we have a quadratic equation of the form
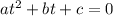`at^(2)+bt+c=0`, which can be solved with the following formula:

`t=\frac{-b \pm \sqrt{b^(2)-4ac}}{2a}`

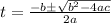
Where:

`a=4.9`

`b=-5`

`c=-40`

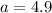
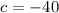
Substituting the known values:

`t=\frac{-(-5) \pm \sqrt{(-5)^(2)-4(4.9)(-40)}}{2(4.9)}`

Solving the equation and choosing the positive result we have:

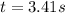`t=3.41 s` This is the time the ball is in air