Question

Which glide reflection describes the mapping ABC DEF?

(x, y) --- (x – 4, y – 1) and reflected across y = 0

(x, y) --- (x – 4, y – 1) and reflected across x = 0

(x, y) --- (x – 1, y + 3) and reflected across y = -3

(x, y) --- (x – 1, y + 3) and reflected across x = -3

Answer 1

A. (x, y) --- (x – 4, y – 1) and reflected across y = 0

Explanation:

Triangle ABC has vertices at points A(-2,-3), B(1,1) and C(1,-3).

1. Translate this triangle 4 units to the left and 1 unit down according to the rule:

`(x,y)\rightarrow (x-4,y-1)`

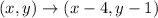
Then

`A(-2,-3)\rightarrow A'(-6,-4);\\ \\B(1,1)\rightarrow B'(-3,0);\\ \\C(1,-3)\rightarrow C'(-3,-4).`

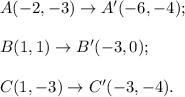
2. Reflect triangle A'B'C' across the x-axis (x-axis has the equation y = 0). The rule of this reflection is

`(x,y)\rightarrow (x,-y)`

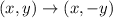
Then

`A'(-6,-4)\rightarrow D(-6,4);\\ \\B'(-3,0)\rightarrow E(-3,0);\\ \\C'(-3,-4)\rightarrow F(-3,4).`