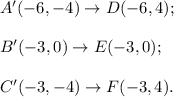Answer:
A. (x, y) --- (x – 4, y – 1) and reflected across y = 0
Explanation:
Triangle ABC has vertices at points A(-2,-3), B(1,1) and C(1,-3).
1. Translate this triangle 4 units to the left and 1 unit down according to the rule:
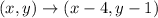
Then
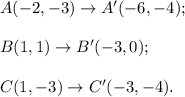
2. Reflect triangle A'B'C' across the x-axis (x-axis has the equation y = 0). The rule of this reflection is
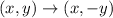
Then