Question

A storage shed is to be built in the shape of a (closed) box with a square base. It is to have a volume of 150 cubic feet. The concrete for the base costs $4 per square foot, the material for the roof costs $2 per square foot, and the material for the sides costs $2.50 per square foot. Express the cost of the material as a function of the (length of the) side of the base.

Answer 1

`C(s) = 6s^2 + (1500)/(s)\\\text{where s is the side of base.}`

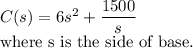
Explanation:

We are given the following in the question:

A storage shed is to be built in the shape of a (closed) box with a square base.

Volume = 150 cubic feet

Let s be the edge of square base and h be the height.

Volume of cuboid =

`l* b* h`

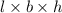
where l is the length, b is the base and h is the height.

Volume of box =

`s^2h = 150\\\\h = (150)/(s^2)`

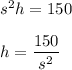
Area of base =

`\text{side}* \text{side} = s^2`

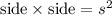
Cost of concrete for the base = $4

Cost of base($) =
`4s^2`

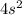
Area of roof =

`\text{side}* \text{side} = s^2`

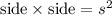
Cost of material for the roof = $2

Cost of roof ($) =
`2s^2`

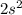
Area of 4 walls =

`4* (sh)\\=4sh`

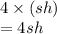
Cost of material for the side = $2.50

Cost of material of side($) =

`2.50* 4s((150)/(s^2))\\\\=(1500)/(s)`

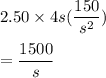
Total cost

= Cost of base + Cost of 4 sides + Cost of roof

`C(s) = 4s^2 + (1500)/(s) + 2s^2\\\\C(s) = 6s^2 + (1500)/(s)`

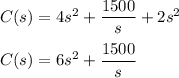
is the required cost function.