Question

Write a polynomial function $f$ of least degree that has rational coefficients, a leading coefficient of 1, and the given zeros. Write the function in standard form -5,-1,2

Answer 1

`f(x) = x^(3) + 4x^(2) -7x^{} -10^{}`

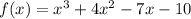
Explanation:

The zeros of the polynomial function are given us as -5,-1,2

If the zeros of a polynomial function are α,β,ω, the polynomial function can be obtained using the expression below:

f(x) = (x - α)(x - β)(x - ω)

where α = -5, β = -1, and ω = 2

`f(x)=(x-(-5) )(x -(-1))(x - 2) = (x+5)(x+1)(x-2)\\\\f(x)=(x+5)(x^(2) -2x + x -2) = (x+5)(x^(2) -x-2)\\\\f(x)=x(x^(2) -x-2)+5(x^(2) -x-2)\\\\f(x)= x^(3) - x^(2) -2x + 5x^(2) - 5x - 10\\\\f(x)= x^(3) + 4x^(2) -7x - 10`

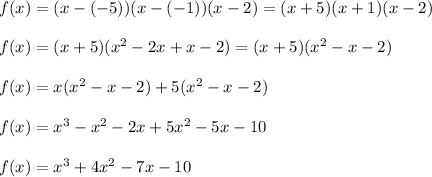
NB: To arrive at the answer, expand the brackets and after expansion, collect like terms to obtain the final answer