Question

The sum of the radius of the base and the height of a solid cylinder is 37m. If the total surface area of the cylinder is 1628 m^2, find its volume

PLEASE HELP

Answer 1

920

Explanation:

Answer 2

4618.14
`m^(3)` or 4618
`m^(3)`

Explanation:

From T.S.A = 2
`\pi`rh + 2
`\pi`
`r^(2)`

where T.S.A = 1628
`m^(2)`

1628 = 2
`\pi`rh + 2
`\pi`
`r^(2)`

1628 = ( rh +
`r^(2)` ) 2
`\pi`

by dividing both side by 2
`\pi`

`(1628)/(2\pi )`= rh +
`r^(2)`

259.10 = rh +
`r^(2)`

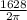rh = 259.10 -
`r^(2)`

h =
`(259.10 - r^(2) )/(r)` (1)

From Radius + Height = 37

r + h = 37 (2)

by substituting eqn 1 into 2

r +
`(259.10 - r^(2) )/(r)` = 37

by multiplying r to both side

`r^(2)` + 259.10 -
`r^(2)` = 37r

259.10 = 37r

r =
`(259.10)/(37)`

r = 7.00 ≅ 7

From Eqn 2

r + h = 37

7 + h = 37

h = 37 - 7

h = 30

so Volume of a cylinder =
`\pi r^(2) h`

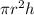
V =
`\pi` *
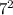`7^(2)` * 30

V = 4618.14
`m^(3)` ≅ 4618
`m^(3)`