Question

What triangle congruency postulate is most applicable for proving the following triangles congruent, using only the information readily available?

Answer 1

Answer:it is SAS

Explanation:

it could be SAS or LL but the anser choices are AAS, ASA, SAS, and HL

Answer 2

See explanation

Explanation:

Consider triangles ABC and ADC. In these triangles,

• 
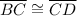  `\overline{BC} \cong \overline {CD}` - given;
• 
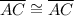  `\overline{AC} \cong \overline {AC}` - reflexive property (this side is common in two triangles);
• 
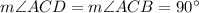  `m\angle ACD=m\angle ACB=90^(\circ)` - the diagram shows two perpendicular lines AC and BD. Perpendicular lines intersect at right angle.

Then two triangles ABC and ADC are congruent by SAS postulate, or two right triangles ABC and ADC are congruent by LL postulate.

SAS postulate states that if two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then these two triangles are congruent.

LL postulate states if the legs of one right triangle are congruent to the legs of another right triangle, then the two right triangles are congruent.