Question

What is the length of the hypotenuse of the triangle?

Triangle A B C. Side A C is 7 feet and side C B is 4 feet. Hypotenuse A B is unknown.
StartRoot 22 EndRoot ft
StartRoot 33 EndRoot ft
StartRoot 57 EndRoot ft
StartRoot 65 EndRoot ft

Answer 1

The last answer
`√(65)`

Explanation:

`7^2+4^2 = 65`

The formula to find it is
`a^2+b^2=c^2`

so
`√(65)` is correct

Answer 2

• √65 ft (Option D)

⠀

Explanation:

• This is Right Angled Triangle.

⠀

We'll solve this using the Pythagorean Theorem.

⠀

• AC = 7ft which is the Base.

• BC = 4 ft which is the Perpendicular.

• AB is the Hypotenuse.

⠀

We know that,

`{ \longrightarrow \pmb{\qquad \: (AB) {}^(2) = (AC) {}^(2) + ( BC) {}^(2)}}`

⠀

`{ \longrightarrow \sf{\qquad \: (AB) {}^(2) = (7) {}^(2) + ( 4) {}^(2)}}`

⠀

`{ \longrightarrow \sf{\qquad \: (AB) {}^(2) = 49 + 16}}`

⠀

`{ \longrightarrow \sf{\qquad \: (AB) {}^(2) = 65}}`

⠀

`{ \longrightarrow \sf {\pmb {\qquad \: AB}}} = \pmb{ \frak{√(65)}}`

⠀

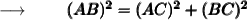
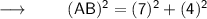
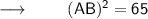
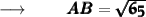
Therefore,

• The length of the Hypotenuse (AB) is √65 ft