Answer:
The proportion of U.S. households that owned two or more televisions is 83%.
Explanation:
To determine whether the proportions of U.S. households that owned two or more televisions is less than 83% or not let us perform a hypothesis test for single proportion.
Assumptions:
The sample size (n) selected by the local cable company is 300 which is quite large. Then according to the Central limit theorem the sampling distribution of sample proportion follows a normal distribution with mean p and standard deviation
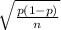 .
.
Since the sampling distribution of sample proportions follows a normal distribution use the z-test for one proportion to perform the test.
The hypothesis is:
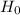 : The proportion of U.S. households that owned two or more televisions is 83%, i.e.
: The proportion of U.S. households that owned two or more televisions is 83%, i.e.
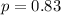
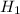 :The proportion of U.S. households that owned two or more televisions is less than 83%, i.e.
:The proportion of U.S. households that owned two or more televisions is less than 83%, i.e.
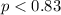
Decision Rule:
At the level of significance α = 0.05 the critical region for a one-tailed z-test is:

**Use the z table for the critical values.
So, if
 the null hypothesis will be rejected.
the null hypothesis will be rejected.
Test statistic value:
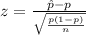
Here
 is the sample proportion.
is the sample proportion.
Compute the value of
 as follows:
as follows:
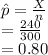
Now compute the value of the test statistic as follows:
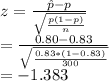
The test statistic is -1.383 which is more than -1.645.
Thus, the test statistic lies in the acceptance region.
Hence we fail to reject the null hypothesis.
Conclusion:
At 0.05 level of significance we fail to reject the null hypothesis stating that the proportion of U.S. households that owned two or more televisions is 83%.