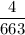Question

You draw two cards from a standard deck of 52 cards and do not replace the first one before drawing the second. Find the probability of drawing a 7 for the first card and a king for the second card. Round your answer to the nearest thousandth.

Answer 1

Answer:
`(4)/(663)`

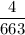
Explanation:

Total number of cards in a deck = 52

Number of cards having 7 on them = 4

Number of cards having king on them = 4

P(a 7 for first card)=
`(4)/(52)=(1)/(13)`

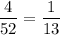
Total cards left = 52-1=51

P( a 7 for first card | a king for the second card) =
`(4)/(51)`

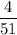
Since , P(A and B) = P(B|A) X P(A) [Conditional probability ]

Now , the probability of drawing a 7 for the first card and a king for the second card. = P( a king for the second card | a 7 for first card ) x (P(a 7 for first card))

`=(1)/(13)*(4)/(51)=(4)/(663)`

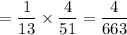
Hence, the required probability :
`(4)/(663)`