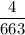Answer:
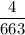
Explanation:
Total number of cards in a deck = 52
Number of cards having 7 on them = 4
Number of cards having king on them = 4
P(a 7 for first card)=
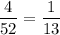
Total cards left = 52-1=51
P( a 7 for first card | a king for the second card) =
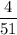
Since , P(A and B) = P(B|A) X P(A) [Conditional probability ]
Now , the probability of drawing a 7 for the first card and a king for the second card. = P( a king for the second card | a 7 for first card ) x (P(a 7 for first card))
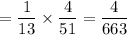
Hence, the required probability :