Answer:
The volume of remaining sphere is 489.84 cubic inches.
Explanation:
We are given the following in the question:
A hole 2 inches in radius is drilled out of a solid sphere of radius 5 inches.
Radius of sphere = 5 inches
Radius of hole = 2 inches
Volume of sphere =
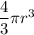
where r is the radius of sphere.
Volume of sphere =
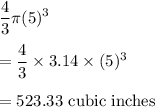
Volume of hole =

Volume of remaining solid =
Volume of sphere - Volume of hole
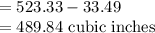
The volume of remaining sphere is 489.84 cubic inches