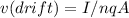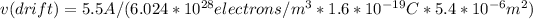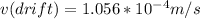Question

An aluminum wire having a cross-sectional area equal to 5.40 10-6 m2 carries a current of 5.50 A. The density of aluminum is 2.70 g/cm3. Assume each aluminum atom supplies one conduction electron per atom. Find the drift speed of the electrons in the wire.

Answer 1

Drift speed of electrons will be 1.056x10^-4 m/s

Step-by-step explanation

Given Data:

A(area)= 5.4 x 10^-6
`m^(2)`

I(current)= 5.5 A

Density= 2.7
`g/cm^(3)`

Calculation:

The equation for drift velocity is:

`v(drift)=I/nqA`

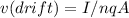
In this case 'q' will be charge of electron which is= 1.6 x 10-19

As each atoms supplies one conduction electron, so number of conduction electrons will be equal to number of atoms.

Hence,

n= no. of conduction electrons/
`m^(3)` = no. of atoms/
`m^(3)`

To find 'n' we can use following equation:

`n= (mass/cm^(3) *atoms/mol)/(mass/mol)`

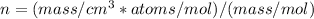
We know atoms/mol is equal to Avogadro`s number i.e 6.02 x 10^23

and molar mass of aluminium is 26.982 g.

Now,

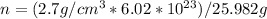`n=(2.7g/cm^(3) * 6.02*10^(23) )/25.982g` (putting values in above equation)

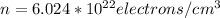
`n=6.024*10^(22) electrons/cm^(3)`

`n= 6.024*10^(22) *10^(6) electrons/m^(3)` (converting electrons/cm3 to electrons/m3)

`n= 6.024*10^(28) electrons/m^(3)`

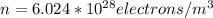
To find drift velocity, we will use equations mention before:

`v(drift)=I/nqA`

`v(drift)=5.5A/(6.024*10^(28)electrons/m^(3) *1.6*10^(-19)C* 5.4*10^(-6)m^(2) )`

`v(drift)= 1.056*10^(-4) m/s`