Question

If the graph f(x)= 9x^2+36x+41/3x+5 has an oblique asymptote at y=3x+k what is the value of k

Answer 1

7

Step-by-step explanation:

Correct on EDGE

Answer 2

• The value of k is 7.

Step-by-step explanation:

To find the oblique asymptote of a rational function you divide the numerator by the denominator and take the quotient (not the remainder).

Such quotient (without the remainder) is the equation of the line that is the oblique asymptote of the rational function.

The rational function is:

`(9x^2+36x+41)/(3x+5)`

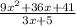
You can see the long division in the picture attached. The quotient is 3x + 7.

Hence, by comparison with y = 3x + k, k = 7.