Question

Suppose the coefficient matrix of a linear system of four equations in four variables has a pivot in each column. Explain why the system has a unique solution. What must be true of a linear system for it to have a unique​ solution? Select all that apply.

Answer 1

If the coefficient matrix has a pivot in each column, it means that it is shaped like this:

`A=\left[\begin{array}{cccc}a_(1,1)&a_(1,2)&a_(1,3)&a_(1,4)\\0&a_(2,2)&a_(2,3)&a_(2,4)\\0&0&a_(3,3)&a_(3,4)\\0&0&0&a_(4,4)\end{array}\right]`

So, the correspondant system

`Ax = b`

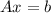
will look like this:

`\left[\begin{array}{cccc}a_(1,1)&a_(1,2)&a_(1,3)&a_(1,4)\\0&a_(2,2)&a_(2,3)&a_(2,4)\\0&0&a_(3,3)&a_(3,4)\\0&0&0&a_(4,4)\end{array}\right]\cdot \left[\begin{array}{c}x_1\\x_2\\x_3\\x_4\end{array}\right] = \left[\begin{array}{c}b_1\\b_2\\b_3\\b_4\end{array}\right]`

This turn into the following system of equations:

`\begin{cases}a_(1,1)x_1+a_(1,2)x_2+a_(1,3)x_3+a_(1,4)x_4=b_1\\a_(2,2)x_2+a_(2,3)x_3+a_(2,4)x_4=b_2\\a_(3,3)x_3+a_(3,4)x_4=b_3\\a_(4,4)x_4=b_4\end{cases}`

The last equation is solvable for
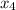`x_4`: we easily have

`x_4=(b_4)/(a_(4,4))`

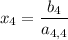
Once the value for
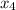`x_4` is known, we can solve the third equation for
`x_3`:

`x_3 = (b_3-a_(3,4)x_4)/(a_(3,3))`

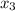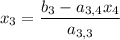
(recall that
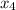`x_4` is now known)

The pattern should be clear: you can use the last equation to solve for
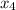`x_4`. Once it is known, the third equation involves the only variable
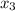`x_3`. Once