If the coefficient matrix has a pivot in each column, it means that it is shaped like this:
![A=\left[\begin{array}{cccc}a_(1,1)&a_(1,2)&a_(1,3)&a_(1,4)\\0&a_(2,2)&a_(2,3)&a_(2,4)\\0&0&a_(3,3)&a_(3,4)\\0&0&0&a_(4,4)\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/8p68vhqmtjcsaq8e2ze232vrko9ux5miic.png)
So, the correspondant system
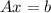
will look like this:
![\left[\begin{array}{cccc}a_(1,1)&a_(1,2)&a_(1,3)&a_(1,4)\\0&a_(2,2)&a_(2,3)&a_(2,4)\\0&0&a_(3,3)&a_(3,4)\\0&0&0&a_(4,4)\end{array}\right]\cdot \left[\begin{array}{c}x_1\\x_2\\x_3\\x_4\end{array}\right] = \left[\begin{array}{c}b_1\\b_2\\b_3\\b_4\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/nf6yhqmr2159qetjodt0851oqi0cs4gn5j.png)
This turn into the following system of equations:
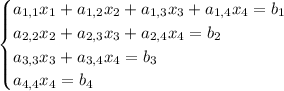
The last equation is solvable for
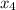 : we easily have
: we easily have
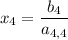
Once the value for
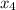 is known, we can solve the third equation for
is known, we can solve the third equation for
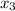 :
:
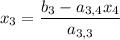
(recall that
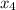 is now known)
is now known)
The pattern should be clear: you can use the last equation to solve for
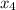 . Once it is known, the third equation involves the only variable
. Once it is known, the third equation involves the only variable
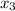 . Once
. Once