Answer:
The number of boys in the course will be = 140
Step-by-step explanation:
Given:
Total number of students enrolled in an introductory biology course = 364
There are 5 boys to every 8 girls in the course.
To find how many boys are in the course.
Solution:
Since, there are 5 boys to every 8 girls in the course.
So, ratio of boys to girls enrolled in the course = 5 : 8
Let the number of boys in the course be =
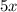
Then number of girls in the course will be =
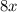
Total number of students would be given as:
⇒ Number of boys + Number of girls
⇒
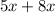
⇒
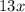
Total number of students given = 364.
Thus, we have:
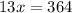
solving for

Dividing both sides by 13.
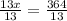
∴
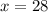
So, number of boys in the course will be =
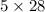 = 140
= 140