Question

Everybody in Ourtown is a fool or a knave or possibly both. 70% of the citizens are foolsand 85% are knaves. One citizen is randomly selected to be mayor. What is the probabilitythat the mayor is both a fool and a knave?

Answer 1

`P( F \cap K) =0.7+0.85 -1=0.55`

Explanation:

For this case we can define some notation first:

F ="One person is fool "

K="One person is knave"

And we have the following probabilities given:

`P(F) = 0.7 , P(K) =0.85`

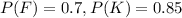
And from the given condition that everyone is fool or knave we can deduce that:

`P(K UF) =1`

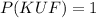
Solution to the problem

For this case we want to find this probability:

`P( F \cap K)`

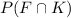
And we can use the total probability rule given by:

`P(K \cup F) = P(F) +P(K) -P(K \cap F)`

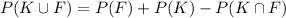
And replacing the values that we have we got:

`1 = 0.7+0.85 -P(K \cap F)`

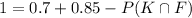
And if we solve for
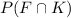`P( F \cap K)` we got:

`P( F \cap K) =0.7+0.85 -1=0.55`