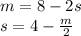For this case we have the following equation:
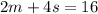
We solve for each of the variables:
For m:
We subtract 4s from both sides of the equation:
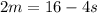
We divide by 2 on both sides of the equation:
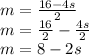
For s:
We subtract 2m from both sides of the equation:
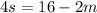
We divide between 4 on both sides of the equation:
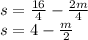
Answer: