Answer :
(A) The dissociation reaction of
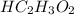 will be:
will be:
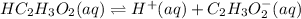
The equilibrium expression :
![K_a=([H^+][C_2H_3O_2^-])/([HC_2H_3O_2])](https://img.qammunity.org/2021/formulas/chemistry/high-school/hyr691u8oh6uqe8k0q2ssk9spq6c7h3d72.png)
(B) The dissociation reaction of
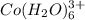 will be:
will be:
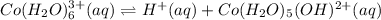
The equilibrium expression :
![K_a=([H^+][Co(H_2O)_5(OH)^(2+)])/([Co(H_2O)_6^(3+)])](https://img.qammunity.org/2021/formulas/chemistry/high-school/qcdw66xk9md8asptwomn5kkviq090egsoe.png)
(C) The dissociation reaction of
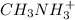 will be:
will be:
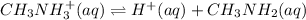
The equilibrium expression :
![K_a=([H^+][CH_3NH_2])/([CH_3NH_3^+])](https://img.qammunity.org/2021/formulas/chemistry/high-school/krtkk7w56a9xbrr35eitnmtb7l3pij0nts.png)
Explanation :
Equilibrium constant : It is defined as the equilibrium constant. It is defined as the ratio of concentration of products to the concentration of reactants.
The equilibrium expression for the reaction is determined by multiplying the concentrations of products and divided by the concentrations of the reactants and each concentration is raised to the power that is equal to the coefficient in the balanced reaction.
As we know that the concentrations of pure solids and liquids are constant that is they do not change. Thus, they are not included in the equilibrium expression.
(A) The dissociation reaction of
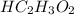 will be:
will be:
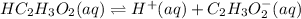
The equilibrium expression of
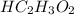 will be:
will be:
![K_a=([H^+][C_2H_3O_2^-])/([HC_2H_3O_2])](https://img.qammunity.org/2021/formulas/chemistry/high-school/hyr691u8oh6uqe8k0q2ssk9spq6c7h3d72.png)
(B) The dissociation reaction of
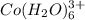 will be:
will be:
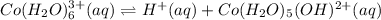
The equilibrium expression of
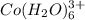 will be:
will be:
![K_a=([H^+][Co(H_2O)_5(OH)^(2+)])/([Co(H_2O)_6^(3+)])](https://img.qammunity.org/2021/formulas/chemistry/high-school/qcdw66xk9md8asptwomn5kkviq090egsoe.png)
(C) The dissociation reaction of
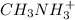 will be:
will be:
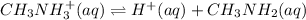
The equilibrium expression of
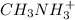 will be:
will be:
![K_a=([H^+][CH_3NH_2])/([CH_3NH_3^+])](https://img.qammunity.org/2021/formulas/chemistry/high-school/krtkk7w56a9xbrr35eitnmtb7l3pij0nts.png)