Question

Complete the dissociation reaction and the corresponding Ka equilibrium expression for each of the following acids in water. (Type your answer using the format [NH4]+ for NH4+ and [Ni(CN)4]2- for Ni(CN)42-. Use the lowest possible coefficients.)

(A) HC2H3O2
HC2H3O2(aq) (twosidedarrow) [ ]H+(aq) + [ ] [ ](aq)
Ka = [ ][ ] / [ ]
(B) Co(H2O)63+
Co(H2O)63+(aq) (twosidedarrow) [ ]H+(aq) +[ ][ ](aq)
Ka = [ ][ ] / [ ]
(C) CH3NH3+
CH3NH3+(aq) (twosidedarrow) [ ]H+(aq) +[ ][ ](aq)
Ka = [ ][ ] / [ ]

Answer 1

The dissociation reactions for acetic acid, hexaaquacobalt(III) ion, and methylammonium along with their Ka equilibrium expressions show how each acid disassociates into its constituent ions in water, and how the concentration of these ions at equilibrium can be represented.

Step-by-step explanation:

Completing the dissociation reaction and the Ka equilibrium expression for each of the following acids in water:

(A) Acetic acid
`($\text{HC}_2\text{H}_3\text{O}_2$)`

`\[\text{HC}_2\text{H}_3\text{O}_2(\text{aq}) \rightleftharpoons \text{H}^+(\text{aq}) + \text{C}_2\text{H}_3\text{O}_2^-(\text{aq})\\\\K_a = \frac{[\text{H}^+][\text{C}_2\text{H}_3\text{O}_2^-]}{\text{HC}_2\text{H}_3\text{O}_2}\]`

(B) Hexaaquacobalt(III) ion
`($\text{Co(H}_2\text{O)}_6^(3+)$)`

`\[\text{Co(H}_2\text{O)}_6^(3+)(\text{aq}) \rightleftharpoons \text{H}^+(\text{aq}) + \text{Co(H}_2\text{O)}_5\text{OH}_2^+(\text{aq})\\\\K_a = \frac{[\text{H}^+][\text{Co(H}_2\text{O)}_5\text{OH}_2^+]}{\text{Co(H}_2\text{O)}_6^(3+)}\]`

(C) Methylammonium
`($\text{CH}_3\text{NH}_3^+$)`

`\[\text{CH}_3\text{NH}_3^+(\text{aq}) \rightleftharpoons \text{H}^+(\text{aq}) + \text{CH}_3\text{NH}_2(\text{aq})\\\\K_a = \frac{[\text{H}^+][\text{CH}_3\text{NH}_2]}{\text{CH}_3\text{NH}_3^+}\]`

Answer 2

(A) The dissociation reaction of
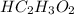`HC_2H_3O_2` will be:

`HC_2H_3O_2(aq)\rightleftharpoons H^+(aq)+C_2H_3O_2^-(aq)`

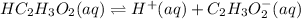
The equilibrium expression :

`K_a=([H^+][C_2H_3O_2^-])/([HC_2H_3O_2])`

(B) The dissociation reaction of
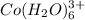`Co(H_2O)_6^(3+)` will be:

`Co(H_2O)_6^(3+)(aq)\rightleftharpoons H^+(aq)+Co(H_2O)_5(OH)^(2+)(aq)`

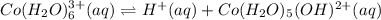
The equilibrium expression :

`K_a=([H^+][Co(H_2O)_5(OH)^(2+)])/([Co(H_2O)_6^(3+)])`

(C) The dissociation reaction of
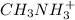`CH_3NH_3^+` will be:

`CH_3NH_3^+(aq)\rightleftharpoons H^+(aq)+CH_3NH_2(aq)`

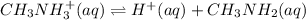
The equilibrium expression :

`K_a=([H^+][CH_3NH_2])/([CH_3NH_3^+])`

Explanation :

Equilibrium constant : It is defined as the equilibrium constant. It is defined as the ratio of concentration of products to the concentration of reactants.

The equilibrium expression for the reaction is determined by multiplying the concentrations of products and divided by the concentrations of the reactants and each concentration is raised to the power that is equal to the coefficient in the balanced reaction.

As we know that the concentrations of pure solids and liquids are constant that is they do not change. Thus, they are not included in the equilibrium expression.

(A) The dissociation reaction of
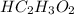`HC_2H_3O_2` will be:

`HC_2H_3O_2(aq)\rightleftharpoons H^+(aq)+C_2H_3O_2^-(aq)`

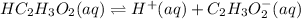
The equilibrium expression of
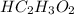`HC_2H_3O_2` will be:

`K_a=([H^+][C_2H_3O_2^-])/([HC_2H_3O_2])`

(B) The dissociation reaction of
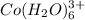`Co(H_2O)_6^(3+)` will be:

`Co(H_2O)_6^(3+)(aq)\rightleftharpoons H^+(aq)+Co(H_2O)_5(OH)^(2+)(aq)`

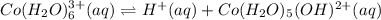
The equilibrium expression of
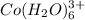`Co(H_2O)_6^(3+)` will be:

`K_a=([H^+][Co(H_2O)_5(OH)^(2+)])/([Co(H_2O)_6^(3+)])`

(C) The dissociation reaction of
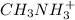`CH_3NH_3^+` will be:

`CH_3NH_3^+(aq)\rightleftharpoons H^+(aq)+CH_3NH_2(aq)`

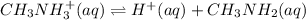
The equilibrium expression of
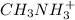`CH_3NH_3^+` will be:

`K_a=([H^+][CH_3NH_2])/([CH_3NH_3^+])`