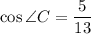Question

Analyze the diagram and complete the instructions that follow find cos C

Answer 1

The Correct option is A.
`(5)/(13)`

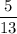
Therefore the value of Cos ∠C is

`\cos \angle C = (5)/(13)`

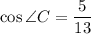
Explanation:

Given:

In Right Angle Triangle ABC

∠B = 90°

BC = 10 ...Adjacent Side to Angle C.

AC = 26 ...Hypotenuse

To Find:

Cos C =?

Solution:

In Right Angle Triangle ABC , By Cosine Identity we have

`\cos C = \frac{\textrm{side adjacent to angle C}}{Hypotenuse}\\`

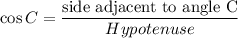
Substituting the values we get

`\cos C = (BC)/(AC)=(10)/(26)=(5)/(13)`

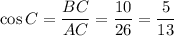
Therefore the value of Cos ∠C is

`\cos \angle C = (5)/(13)`