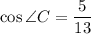Answer:
The Correct option is A.
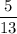
Therefore the value of Cos ∠C is
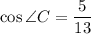
Explanation:
Given:
In Right Angle Triangle ABC
∠B = 90°
BC = 10 ...Adjacent Side to Angle C.
AC = 26 ...Hypotenuse
To Find:
Cos C =?
Solution:
In Right Angle Triangle ABC , By Cosine Identity we have
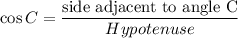
Substituting the values we get
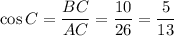
Therefore the value of Cos ∠C is