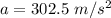Answer
given,
torque produced, τ = 22 N.m
Radius of the wheel. r = 10 cm
Moment of inertial = 2 kg.m²
initial angular speed = 0 rad/s
time, t = 5 s
a) we know,
τ = I α
22 = 2 x α
α = 11 rad/s²
using equation of rotation motion
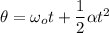

θ = 137.5 rad
θ = 137.5/2π = 22 revolution.
b) angular velocity of the motor
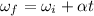
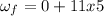
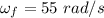
c) acceleration of a point on the rim of the wheel
radial acceleration


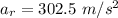
tangential acceleration of the point on the rim
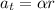
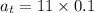
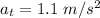
now, acceleration of the point