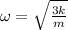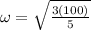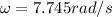To develop this problem we will be guided by the graph that fits the description of the problem. Performing sum of torques we will find the displacement of the body after the displacement of a small angle, this would be
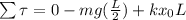
Here
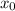 = the equilibrium compression
= the equilibrium compression
After displacement by a small angle
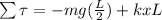
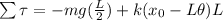
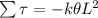
At the same time we have that the angular torque can be defined as,
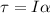
Here,
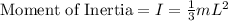
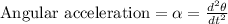
Replacing this value we have that
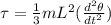
Replacing the previous value for the angular torque found,
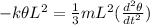
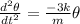
Angular acceleration is opposite in direction and proportional to the displacement so we have simple harmonic motion with
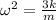
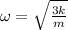
PART B) Evaluating for m = 5kg and k = 100N/m we have that