Answer:
Radius of the larger circle is approximately 4.52 m.
Explanation:
Given:
Sum of area of 2 circle = 80 sq. m
Let the radius of smaller circle be 'r'.
Then Given:
one of them is twice as long as the other.
radius of the Larger circle =
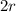
we need to find the radius of the larger circle.
Solution:
Now we know that;
Area of the circle is π times square of the radius.
framing in equation form we get;
Area of the smaller circle =

Area of larger circle =
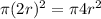
Now given:
Area of the smaller circle + Area of the larger circle = 80
Substituting the values we get;
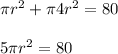
Now Dividing both side by 5π we get;
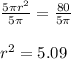
Taking square root on both side we get;
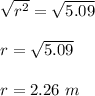
Now radius of larger circle =
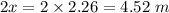
Hence Radius of the larger circle is approximately 4.52 m.