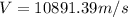Question

With what speed must a satellite be moving in order to maintain a

circular orbit 3360 km above the surface of the Earth?

Answer 1

Answer:
`V=10891.39 m/s`

Step-by-step explanation:

Since we are told the satellite movs in a circular orbit, we can use the equation of velocity in the case of uniform circular motion:

`V=\sqrt{G(M)/(r)}`

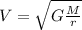
Where:

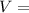`V=` is the velocity of the satellite

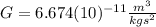`G=6.674(10)^(-11)(m^(3))/(kgs^(2))` is the Gravitational Constant

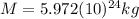`M=5.972(10)^(24) kg` is the mass of the Earth

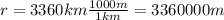`r=3360 km (1000 m)/(1 km)=3360000 m` is the radius of the orbit

Solving with the given data:

`V=\sqrt{6.674(10)^(-11)(m^(3))/(kgs^(2))(5.972(10)^(24) kg)/(3360000 m)}`

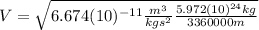
Finally:

`V=10891.39 m/s`