Question

Derive sina

`derive \: (sin(cos ^(2) x)) \:`
​

Answer 1

the derivative of given function is

`cos(cos^2 x )(-sin 2 x)`

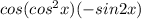
Explanation:

Step :-

using chain rule formula
`(d y)/(d x) = (d y)/(d u) X(d u)/(d x)`

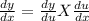
let
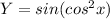`Y = sin(cos^2 x)` ...........(1)

`(d(sin x))/(d x) = cos x`

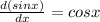
Differentiating equation (1) with respective to x,we get

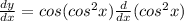`(d y)/(d x) = cos(cos^2 x) (d)/(d x) (cos^2 x)`........(2)

we will use again formula

`(d(cos x))/(d x) = -sin x`

`(d (x^(2) ))/(d x) =2 x`

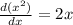
From (2) equation we will get solution is

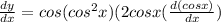`(d y)/(d x) = cos (cos^2 x) (2 cos x ((d(cos x))/(dx) )` ........(3)

again simplification the equation (3) we will get

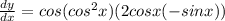`(d y)/(d x) = cos(cos^2 x)(2 cos x(-sin x))` ........(4)

by using trigonometry formula

`2 sin x cos x = sin2x`

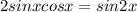
now the equation (4) we get final solution is

`(d y)/(d x) = cos(cos^2 x)(- sin2x)`