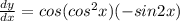Answer:
the derivative of given function is
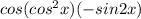
Explanation:
Step :-
using chain rule formula
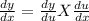
let
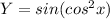 ...........(1)
...........(1)
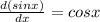
Differentiating equation (1) with respective to x,we get
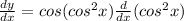 ........(2)
........(2)
we will use again formula
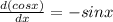
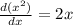
From (2) equation we will get solution is
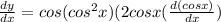 ........(3)
........(3)
again simplification the equation (3) we will get
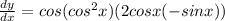 ........(4)
........(4)
by using trigonometry formula
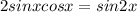
now the equation (4) we get final solution is