Answer:
Given function:
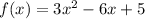
Vertex form:
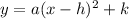
(where
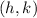 is the vertex)
is the vertex)
Expand vertex form:
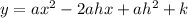
Compare coefficients of given function with expanded vertex form
Comparing coefficient of
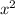 :
:
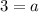
Comparing coefficient of
 :
:
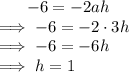
Comparing constant:
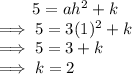
Therefore, the vertex is (1, 2)
As the leading coefficient is positive, the parabola will open upwards.
Additional plot points:


(0, 5) and (2, 5)